

您访问的链接即将离开“江门市人民政府门户网站” 是否继续?
继续访问放弃



































 85566
85566
 15
2025-05-14 14:03:01
15
2025-05-14 14:03:01



 33274
33274
 72
2025-05-14 14:03:01
72
2025-05-14 14:03:01



 63768
63768
 52
2025-05-14 14:03:01
52
2025-05-14 14:03:01


 31596
31596
 16
2025-05-14 14:03:01
16
2025-05-14 14:03:01



 24832
24832
 83
2025-05-14 14:03:01
83
2025-05-14 14:03:01



 17804
17804
 74
2025-05-14 14:03:01
74
2025-05-14 14:03:01



 51146
51146
 62
2025-05-14 14:03:01
62
2025-05-14 14:03:01



 40289
40289
 66
2025-05-14 14:03:01
66
2025-05-14 14:03:01


 42194
42194
 65
2025-05-14 14:03:01
65
2025-05-14 14:03:01



 47586
47586
 87
2025-05-14 14:03:01
87
2025-05-14 14:03:01



 22063
22063
 23
2025-05-14 14:03:01
23
2025-05-14 14:03:01



 24022
24022
 31
2025-05-14 14:03:01
31
2025-05-14 14:03:01


 11996
11996
 83
2025-05-14 14:03:01
83
2025-05-14 14:03:01



 34888
34888
 45
2025-05-14 14:03:01
45
2025-05-14 14:03:01


 88083
88083
 76
2025-05-14 14:03:01
76
2025-05-14 14:03:01



 48895
48895
 26
2025-05-14 14:03:01
26
2025-05-14 14:03:01



 57094
57094
 21
2025-05-14 14:03:01
21
2025-05-14 14:03:01


 36896
36896
 28
2025-05-14 14:03:01
28
2025-05-14 14:03:01


 14550
14550
 41
2025-05-14 14:03:01
41
2025-05-14 14:03:01



 79191
79191
 47
2025-05-14 14:03:01
47
2025-05-14 14:03:01



 35087
35087
 16
2025-05-14 14:03:01
16
2025-05-14 14:03:01



 47975
47975
 23
2025-05-14 14:03:01
23
2025-05-14 14:03:01



 67560
67560
 37
2025-05-14 14:03:01
37
2025-05-14 14:03:01



 25710
25710
 85
2025-05-14 14:03:01
85
2025-05-14 14:03:01



 72390
72390
 25
2025-05-14 14:03:01
25
2025-05-14 14:03:01



 31796
31796
 24
2025-05-14 14:03:01
24
2025-05-14 14:03:01



 42479
42479
 83
2025-05-14 14:03:01
83
2025-05-14 14:03:01



 85101
85101
 39
2025-05-14 14:03:01
39
2025-05-14 14:03:01



 36271
36271
 75
2025-05-14 14:03:01
75
2025-05-14 14:03:01



 23817
23817
 78
2025-05-14 14:03:01
78
2025-05-14 14:03:01



 23597
23597
 60
2025-05-14 14:03:01
60
2025-05-14 14:03:01



 61373
61373
 85
2025-05-14 14:03:01
85
2025-05-14 14:03:01



 13396
13396
 27
2025-05-14 14:03:01
27
2025-05-14 14:03:01



 71134
71134
 80
2025-05-14 14:03:01
80
2025-05-14 14:03:01



 45153
45153
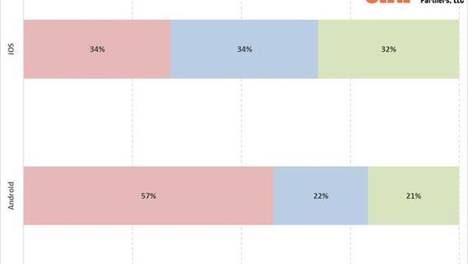 35
2025-05-14 14:03:01
35
2025-05-14 14:03:01


 81949
81949
 30
2025-05-14 14:03:01
30
2025-05-14 14:03:01



 81954
81954
 46
2025-05-14 14:03:01
46
2025-05-14 14:03:01



 89439
89439
 22
2025-05-14 14:03:01
22
2025-05-14 14:03:01



 12889
12889
 59
2025-05-14 14:03:01
59
2025-05-14 14:03:01



 65975
65975
 29
2025-05-14 14:03:01
29
2025-05-14 14:03:01



 35643
35643
 85
2025-05-14 14:03:01
85
2025-05-14 14:03:01



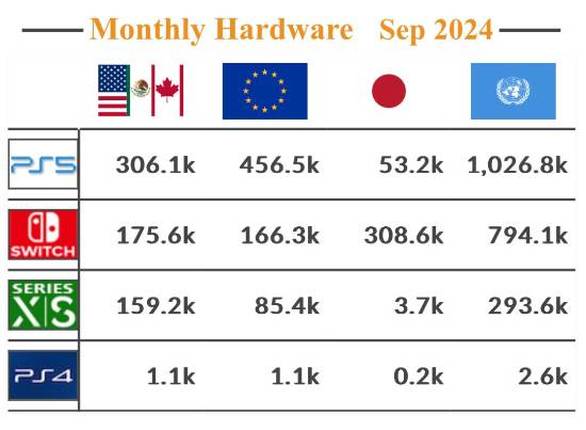 10406
10406
 83
2025-05-14 14:03:01
83
2025-05-14 14:03:01

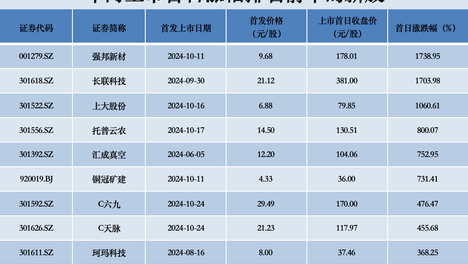

 26432
26432
 34
2025-05-14 14:03:01
34
2025-05-14 14:03:01



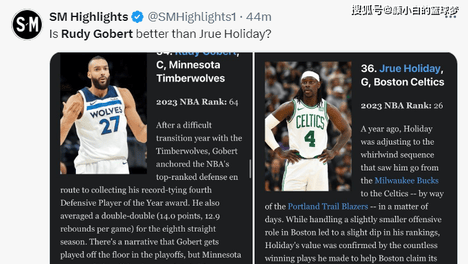 15005
15005
 82
2025-05-14 14:03:01
82
2025-05-14 14:03:01


 59572
59572
 47
2025-05-14 14:03:01
47
2025-05-14 14:03:01



 29807
29807
 58
2025-05-14 14:03:01
58
2025-05-14 14:03:01



 12339
12339
 60
2025-05-14 14:03:01
60
2025-05-14 14:03:01

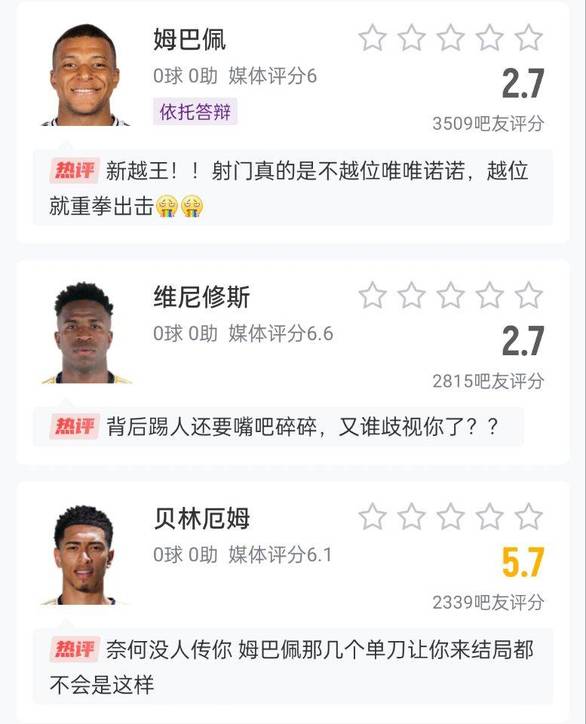

 16232
16232
 74
2025-05-14 14:03:01
74
2025-05-14 14:03:01



 29763
29763
 81
2025-05-14 14:03:01
81
2025-05-14 14:03:01



 39392
39392
 19
2025-05-14 14:03:01
19
2025-05-14 14:03:01



 21790
21790
 25
2025-05-14 14:03:01
25
2025-05-14 14:03:01



 85076
85076
 61
2025-05-14 14:03:01
61
2025-05-14 14:03:01



 41079
41079
 72
2025-05-14 14:03:01
72
2025-05-14 14:03:01



 12956
12956
 40
2025-05-14 14:03:01
40
2025-05-14 14:03:01
| 中国必胜,伊万必败!zhong guo bi sheng ,yi wan bi bai ! | 87天天前 |
| 尼玛老屁眼,骗吃骗喝没商量啊。 | |
| 准备输吧!吃喝玩乐挺厉害的呢!!zhun bei shu ba !chi he wan le ting li hai de ne !! | 74天天前 |
| 实力决定一切,想咸鱼翻身谁信,希望越大伴随着失望更大,散伙吧!免得国人生气。 | |
| 我的预测很准,上此热身赛3:1我是2天前说的。这次是2:0,都是下半场进的球。wo de yu ce hen zhun ,shang ci re shen sai 3:1wo shi 2tian qian shuo de 。zhe ci shi 2:0,dou shi xia ban chang jin de qiu 。 | 48天天前 |
| 沙特认为,又要捏软柿子了 | |
| 问题将出在王漏勺身上,不信等着瞧wen ti jiang chu zai wang lou shao shen shang ,bu xin deng zhe qiao | 36天天前 |
| 学会吹大牛了,必被打脸! | |
| 一万、王地雷,惨案主教练,惨案队长,0:7yi wan 、wang di lei ,can an zhu jiao lian ,can an dui chang ,0:7 | 27天天前 |
| 能不能出线,看看运气,而非实力。 | |
| 侵入领空就该击落qin ru ling kong jiu gai ji luo | 24天天前 |
| 这是一个坑,必须毫不犹豫坚决回答是!击落!! | |
| 军机入侵领空必须歼灭jun ji ru qin ling kong bi xu jian mie | 86天天前 |
| 奇谈怪论,难道我们对入侵们敌人不能反击?! | |
| 侵入领空,先予警告驱离,不听的话直接击落!qin ru ling kong ,xian yu jing gao qu li ,bu ting de hua zhi jie ji luo ! | 32天天前 |
| 这个标题很 耐撕 | |
| 澳大利亚军机进入中国领空 可能遭到军事反击?—————— 肯定要反击!!!正如,民间一个人闯进别人家里,那肯定要受到驱赶,难不成留他吃饭?说:我家你随便进“??!!!扯蛋的澳大利亚!!ao da li ya jun ji jin ru zhong guo ling kong ke neng zao dao jun shi fan ji ?—————— ken ding yao fan ji !!!zheng ru ,min jian yi ge ren chuang jin bie ren jia li ,na ken ding yao shou dao qu gan ,nan bu cheng liu ta chi fan ?shuo :wo jia ni sui bian jin “??!!!che dan de ao da li ya !! | 53天天前 |
| 为什么是可能? | |
| 澳🐩不能惯着ao 🐩bu neng guan zhe | 36天天前 |
| 本质上,澳大利亚是跟着美国反华的,而且是根深蒂固的。只是想在贸易中赚更多的钱! | |